Division Algebra Over Q
X n α is an associative division F -algebra. An ideal of Anot containing 1.

Use Long Division To Divide Polynomials College Algebra
You can put this solution on YOUR website.

Division algebra over q. What are the other examples of Central divison algebras over mathbbQ with the same property. I know that division algebras in the form of mathbbQalpha are just number fields. So we can do this general contruction with F Q.
1 day agoQuaternions over mathbbQ are an example of a Central Division algebra over mathbbQ for which the basis elements ijij other than 1 are represented by skew-symmetric matrices in regular representation. The algebra of n nmatrices M nK over Kis both central and simple. The division algorithm is absolutely essential for us but its proof is.
So xis algebraic over Q if there exists 0 6f2Qt such that fx 0. For example the polynomial f X 3 3 X 1 Q X has discriminant 81 which is a square so its Galois group G has only even permutations. Let denote the dimension of over.
According to the Frobenius theorem all associative finite-dimensional division algebras over the field of real numbers are exhausted by itself the field of complex numbers and the quaternion algebra. Answer by Boreal 13856 Show Source. Show that any division algebra is an algebra over the eld of rational numbers Q or the eld Fp of prime order.
1 is a root so x-1 is a factor. Polynomial Long Division Calculator - apply polynomial long division step-by-step. Exponent a small number 1-64q3-12q48q2 written above and to the right of the base number tells how many times the base number is being multiplied Tiger Algebra Solver.
The most common method for finding how to rewrite quotients like that is polynomial long division. Can this happen if A is a nite dimensional algebra over k. A complex number xthat is not algebraic over Q is called transcen- dental over Q so x2C is transcendental if there exists no nonzero.
Clearly division algebras are simple. We can go on forever doubling in each step the dimension of the algebra. The division algebra Dn is defined by 461D n K nS S n p.
Or get the full course http. Substituting the integer q for the variable x we see that the integer Φ nq divides the integer qn 1qm i nq divides q 1 because it divides all the other terms. Thus Φ nq q 1.
Since f is irreducible we see that G is cyclic of order 3. On the other hand because 1 is the closest point on the unit circle in CC to the positive integer q we have that for every primitive n-th root. Rational Zero Test or Rational Root test provide us with a list of all possible real Zer.
Let k be an algebraically closed eld and D a nite dimensional division algebra over k. The finite dimensional division algebras over mathbbF_q are just the finite field extensions. A K-algebra is a division algebra if every non-zero element a2Ahas an inverse ie there exists b2Asuch that ab 1 ba.
P is 6 and q is 1 the coefficient of x3. Polynomials qx and rx satisfying 1 ax bxqx rx. Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi.
Division Algebras Konrad Voelkel 2015-01-27 Contents 1 Big Picture1 2 Algebras2. Can they all be embedded into mathbbH. If and if is the maximal subfield in then.
A K-algebra Ais central if its center is K. So I was wondering what do we know about finite dimensional field extensions over mathbbQ. Indeed denote by e.
Any quotient of polynomials axbx can be written as qxrxbx where the degree of rx is less than the degree of bx. For a unital composition algebra Awith quadratic form N we define a. It is known to contain each degree n field extension of Qp as a subfield.
It is an algebra over Qp of rank n2 with center Qp. The next step are the Sedenions S which are no longer a division algebra but still power-associative. Brief Division in Algebra video.
Give an example of a ring A and elements ab 2 A such that ab 1 but ba 6 1. 2 This is to be compared with the standard result in the integers that for integers abwith b6 0 there are unique qand rwith a bq rand 0 r. This website uses cookies to ensure you get the best experience.
Therefore the possible integer roots are -1236. Learn how to use the Rational Zero Test on Polynomial expression.

Total 42 Average 3 8 5 Division Algorithm For Polynomials If P X And G X Are Any Two Polynomials With G X 0 Division Algorithm Polynomials Algorithm

546342998550065558 Special Education Math Math Division Teaching Long Division
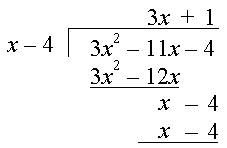
3 Division Of Algebraic Expressions

Octal Division Examples Base 8 Division Division Examples Division Example

Algebra Division Dividing Polynomials Long Division Polynomials Algebraic Expressions Quadratics

Form 2 Unit 2 Lesson 4 Multiplication And Division Of Algebraic Expression Brilliant Maths

Finally How To Use Algebra Tiles For Division Algebra Math Middle School Math

Long Division Notes And Example Long Division Polynomials Math

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Algebra Formulas Algebra Notes Algebra

Indices Harder Questions This Or That Questions Hard Questions Math Worksheets

Division Algorithm For Polynomials A Plus Topper Https Www Aplustopper Com Division Algorithm For Polynomials Pol Division Algorithm Polynomials Algorithm
Normed Division Algebra In Nlab

The Inverse Relationships Multiplication And Division Range 1 To 9 A Ma Algebra Worksheets Addition And Subtraction Worksheets Math Division Worksheets

Algebra 1 Worksheets Basics For Algebra 1 Worksheets Rational Numbers Mathematics Worksheets Subtracting Rational Numbers

Solve For X When X 5 5 X 2 Algebra Equations Math Algebra
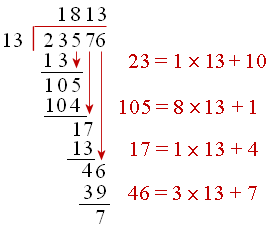
3 Division Of Algebraic Expressions
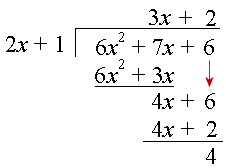
3 Division Of Algebraic Expressions
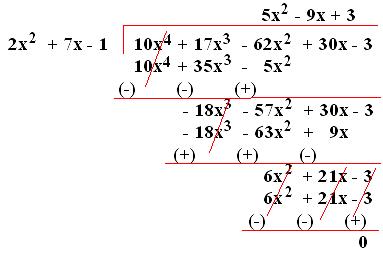
Division Of Algebraic Expression Division Of A Monomial Polynomial

Associate Law By Mel Q Resources Australia Teachers Pay Teachers Classroom Posters Associative Law Teacher Newsletter