Polynomial Division In Finite Field
Dividing polynomials defined over a finite field is a little bit. The polynomial P x4 1 is irreducible over Q but not over any finite field.
Addition And Multiplication In A Galois Field Mathematics Stack Exchange
H f g.

Polynomial division in finite field. Ai F for 0 i n and n 0 along with polynomial addition and multiplication forms a ring and is called the polynomial ring over F. 3 0 mod 3. B 0 1 0 1 1.
However the vertical spacing between each line and exponents of the equation below it is quite small how to increase it. Dividing two polynomials constructs an element of the fraction field which Sage creates automatically. Q is a field with q p n elements where p is a prime number.
It is also common to use the phrase polynomial over a field to convey the same meaning. This tool allows you to carry out algebraic operations on elements of a finite field. Parent Fraction Field of Univariate Polynomial Ring in x over Rational Field.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. In a finite field of order q the polynomial X q X has all q elements of the finite field as roots. I attempted the following solution.
Partial fraction decomposition 2. Q_rvr_rv gfdeconv bap q_rv 14 1 0 0 1. Represent the polynomials using row vectors and divide them in GF 3.
The remainder 3 is then reduced modulo 3. Polynomial fast exponentiation in finite field. This group is cyclic so all non-zero elements can be expressed as powers of a single element called a primitive element of the field.
A 1 1. A finite field K. H x3 1x2 - 17 sage.
Here is the finite field with elements so that for some prime number and integer. To confirm the output compare the original Galois field polynomials to the result of adding the. F x 3 1.
Polynomial factorization with rational coefficients. Polynomial ring rm Fx for rm F a field as above. Polynomial long division is the way to go.
On any field extension of F2 P x 1 4. The elements of Fx are called polynomials over F. For the case where n 1 you can also use Numerical calculator.
Polynomial greatest common divisor. N-degree polynomial roots. The degree of a polynomial is the.
Lets say that the coefficient set is a finite field F with its own rules for addition subtraction multiplication and division and lets further say that when we carry out an arithmetic operation on two polynomials we subject the operations on the coefficients to those that apply to the finite field. For computations over we tacitly assume that we are given a monic irreducible. G x 2 - 17 sage.
In particular these results are studied when one studies normal forms for finitely-generated modules over a PID eg. If not how to manually typeset long division in general. In general there will be several primitive elements for a given field.
Let denote the bit complexity of multiplying two integers of at most bits in the deterministic multitape Turing model Similarly let denote the bit complexity of multiplying two polynomials of degree in. You need to reduce the result from the polynomial operations by modulo the polynomial modulus and then reduce the coefficients modulo the integer modulus. The polynomial division calculator allows you to take a simple or complex expression and find the quotient and remainder instantly.
On every other finite field at least one of 1 2 and 2 is a square because the product of two non-squares is a square and so we have If. 12 Polynomial Rings over Finite Fields Let F be a field. The set Fx Xn i0 aix i.
Especially over a finite field where you dont have to worry about fractional coefficients working over for instance the rational numbers these can get extremely unwieldy surprisingly soon. Square free polynomial factoring in finite field. 2x 2 x 4 x 4 2x 2 you reduce this result by dividing by x 2 -1.
Click the blue arrow to submit and see the result. Enter the expression you want to divide into the editor. Take one of the above examples.
Is there a package like polynom for typesetting polynomial long division but over a finite field such as GF2. When one studies linear systems of equations with coefficients in the non-field. 65 DIVIDING POLYNOMIALS DEFINED OVER A FINITE FIELD First note that we say that a polynomial is defined over a field if all its coefficients are drawn from the field.
Extended polynomial GCD in finite field The calculator computes extended greatest common divisor for two polynomials in finite field. X QQ x. The non-zero elements of a finite field form a multiplicative group.
Finite Fields Of The Form Gf 2n

Finding The Gcd Of Two Polynomials Over A Finite Field Youtube

Division In Finite Fields Mathematics Stack Exchange
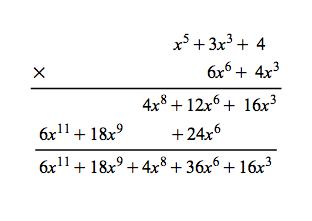
Galois Theorem And Polynomial Arithmetic
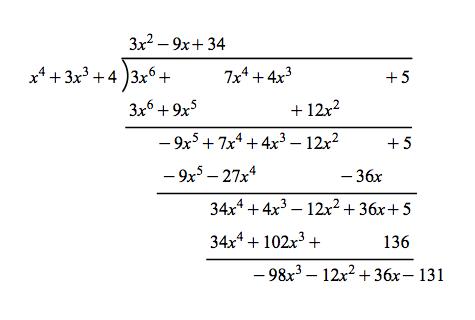
Galois Theorem And Polynomial Arithmetic

Finding The Greatest Common Divisor Of Polynomials Over A Finite Field Youtube
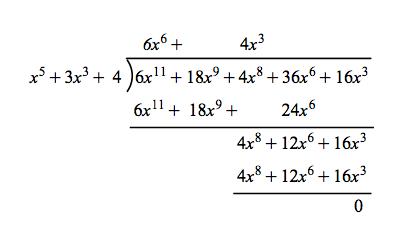
Galois Theorem And Polynomial Arithmetic
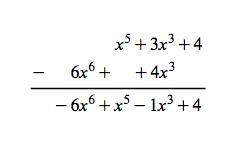
Galois Theorem And Polynomial Arithmetic

Polynomial Long Division Over Gf P Tex Latex Stack Exchange

Section 4 5 Polynomial Arithmetic Cryptography And Network Security 4th Edition
.jpg)
Digital Communication Systems Reed Solomon Galois Fields Theory

Advanced Encryption Standard Aes Sub Stages Finite Field Arithmetic Youtube
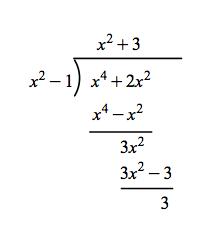
Galois Theorem And Polynomial Arithmetic

Addition And Multiplication In F 4 Mathematics Stack Exchange
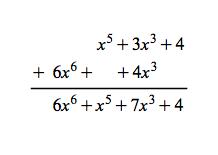
Galois Theorem And Polynomial Arithmetic
