Algebras Over A Division Ring

Division Algebras A division ring is a ring with 1 in which every nonzero element is invertible. FˆM nDthe scalar matrices with entries in F.

Polynomial Division Inb Pages Mrs E Teaches Math Polynomials High School Math Lesson Plans High School Math Lessons

Any division ring is an associative division algebra over its center and has identity but it may not be finite dimensional over its center.

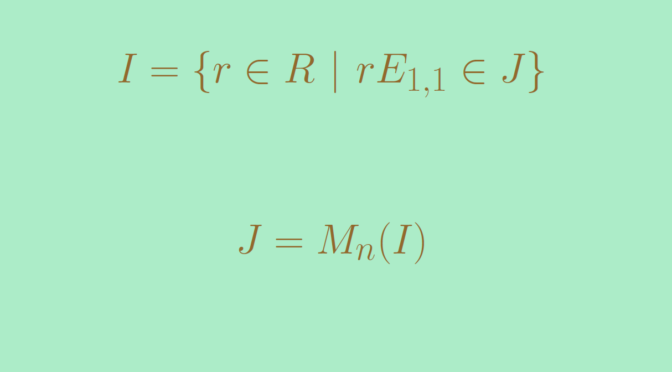
Algebras over a division ring. But I have seen that when we are considering a matrix ring over a division ring which is not necessarily commutative are also named as matrix algebra. The theory of finite-dimensional division. Ignoring scalar multiplication an associative algebra is a ring and a.

We denote by D L the division subring of D L generated by U L. Let be a division ring with the center Let be a finite abelian subgroup of and put It is obvious that is a commutative domain and Also since is finite is a finite dimensional vector space over and thus every element of is algebraic over Let and suppose that is the minimal polynomial of over Then and so Therefore is a field and we are done by the above theorem. An R-algebra is a ring Awith 1 together with a ring homomorphism f.

For an associative division algebra these inverses are equal turning the non-zero vectors into a group under multiplication. If you had a free division ring F on a set X and any division ring R then any set theoretic map Xto R would correspond to a unique division ring homomorphism Fto R. We identify MD with EndM.

In algebra a division ring also called a skew field is a ring in which division is possible. Makar-Limanov himself provided evidence for this in where it is proved that the division ring of fractions of the first Weyl algebra over the rational numbers. Therefore a ring can be regarded as a special case of an algebra.

Skew-fields that are algebras over a certain field are called division algebras cf. Let k be a field of characteristic zero and let L be a nonabelian Lie k -algebra. Let D be a division ring and F a subfield of its center.

Let n t be positive integers. A finite-dimensional unital division algebra is an algebra with multiplicative identity where unique right and left inverses exist for every non-zero element. Let Abe any ring and Ra subring of ZA.

We can also generate Rmore e ciently. I have read that matrix ring over a commutative ring forms an associative algebra so we call the matrix ring as matrix algebra. One reason to consider F-algebras is simply the utility of the extra structure.

An F-algebra Ris in particular an F-vector space which means we can often use dimension-counting arguments. If X has at least two elements xneq y let RmathbbQ. Any ring Ais a Z-algebra in a unique way.

A division algebra over a field K is just a division ring that is also a K-algebra. The ring of rational polynomials mathbb R X is an infinite dimensional real associative division algebra. Then there exists a right AR- WEYL ALGEBRAS OVER DIVISION RINGS 343 module N such that N M if and only if there exists a unital ring homomorphism of AT into the matrix ring MD.

RAis the inclusion mapping. We prove a Wedderburn-Artin type theorem for irreducible F-algebras of F-algebraic matrices in M n DWe then use our result to show that up to a similarity M n F is the only irreducible F-algebra of triangularizable matrices in M n D with inner eigenvalues in F provided that such an F-algebra exists. The pair Af will also be called an R-algebra.

Much of linear algebra may be formulated and remains correct for left modules over division rings instead of vector spaces over fields. Linear maps between finite-dimensional modules over a division ring can be described by matrices and the Gaussian elimination algorithm remains applicable. RAsuch that i f1 R 1 A.

Any ring can be regarded as an algebra over the ring of the integers by taking the product n a where n is an integer to be the usual one that is a dots a n times. Every module over a division ring has a basis. If Dis a division ring containing F in its center then M nDis an F-algebra with.

Cohn constructed a division ring D L that contains U L. Is an R-algebra where. If either L is residually nilpotent or U L is an Ore domain we show that D L contains noncommutative free group algebras.

So division may be defined as a b a b1 but this notation is generally avoided as one may have a b1 b1 a. Ii fR ZA where ZA is the center of A. You may think of a division ring as a field with the axiom of.

Specifically it is a nonzero ring in which every nonzero element a has a multiplicative inverse that is an element generally denoted a1 such that a a1 a1 a 1. Let R be a ring let M be a simple right R-module and set D EndjM. Equiva-lently the only one-sided ideals are the zero ideal and the whole ring.

Every division ring is a division algebra over its center. Over a division ring Dhas a left a right dimension which may be denoted dimVIn 16 Jacobson gives an example of a division ring Dand an abelian group V which is both a right and a left D-vector space such that the left and the right dimensions are not equal.

25 Division Of Algebraic Expressions Solving Questions Youtube

Algebra 2 Worksheets Complex Numbers Worksheets Complex Numbers Simplifying Rational Expressions Algebra Worksheets

Abstract Algebra 1 The Division Algorithm Youtube

Fast Algebra Techniques College Math Education Math Math Methods

Polynomial Long Division In Algebra 2 Teaching Algebra Polynomials Math Methods

Addition Subtraction Elementary Algebra Worksheet Printable Elementary Worksheets Basic Math Worksheets Elementary Algebra

Normed Division Algebra In Nlab

Every Division Ring Is A Simple Ring Theorem Ring Theory Algebra Youtube

What Is A Division Ring Definition And Example Ring Theory Algebra Youtube

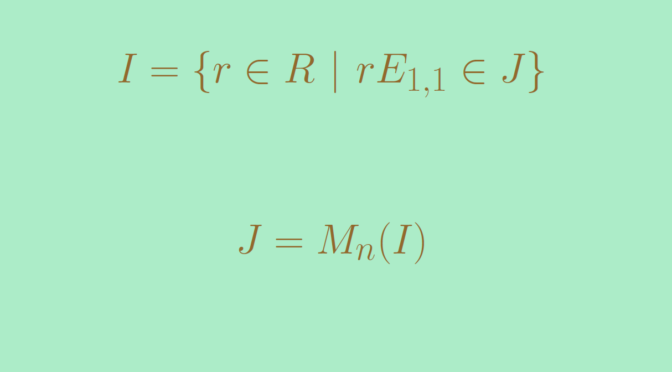
A Simple Ring Which Is Not A Division Ring Math Counterexamples

A Division Ring Has No Zero Divisor Theorem Ring Theory Algebra Youtube

Fast Algebra Techniques College Math Education Math Math Methods

Algebraically Closed Field In A Division Ring Mathematics Stack Exchange

Tai Danae Bradley On Twitter Grad Student Binary Operation Commutative

Fast Algebra Techniques College Math Education Math Math Methods

What Is A Division Ring Definition And Example Ring Theory Algebra Youtube

Fraction Rules Poster Or Handout Studying Math Math Methods Teaching Math

American High School Online School License Oninehighschoolforsale Onlineschoolforsale Virtualscho Online High School Online School Programs Online Education

Division Properties Of Exponents Notes Exponents Negative Exponents Algebra